Depuis les crises pétrolières des années 70 et 80, la littérature économique ne cesse de se questionner sur les liens entre l’évolution des prix pétroliers et la dynamique économique (Herrera et al, 2019). Les produits pétroliers cruciaux dans les processus de production et les coûts de transport, déterminent grandement l’évolution du niveau général des prix au sein de bon nombre d’économie industrialisée. L’évolution des prix pétroliers est donc source d’incertitudes aussi bien au niveau des pouvoirs publics que des agents économiques privés dans leurs décisions d’investissement et de consommation. Elle requiert donc une attention particulière au sein de la littérature et des travaux visant à la décrire ainsi qu’à la prévoir ne cessent d’émerger. De surcroît, la crise du Covid-19 et la crise énergétique qui s’en suit depuis lors remettent en lumière les enjeux liés à la compréhension de la dynamique des prix des produits  énergétiques (Alana et Monge, 2020).

Dans le cadre de ce dossier, nous utilisons des données mensuelles décrivant l’évolution des prix pétroliers en nous questionnant sur la nature de sa dynamique. Plus encore dans quelle mesure la dynamique passé des prix pétroliers peut nous servir de base pour prédire ses valeurs futures. Pour ce faire, nous mobilisons les techniques des séries temporelles à mémoire longue.

La suite de notre travail se décline en trois grandes parties. En premier, une section consacrée à la problématique traitée par ce dossier, et en second une section qui décrit l’approche économétrique adoptée. La troisième section présente les résultats d’estimation et les interprétations associées. Enfin, s’en suivra une brève conclusion.

1.      Problématique

L’évolution des prix pétroliers ne cesse de susciter l’intérêt des pouvoirs publics et de la littérature économique au cours des dernières décennies. En effet, compte tenu de son rôle dans le processus de production et dans la consommation, des questions émergent tant sur les causes des fluctuations qu’elle peut connaître ainsi que sur les conséquences disruptives que cela peut avoir sur l’activité économique.

Concernant les causes des fluctuations que connaissent les prix des produits pétroliers, la littérature peut s’entrevoir en deux courants. Notamment, avant les premières crises pétrolières des années 70, les fluctuations que connaissaient les prix pétroliers étaient vues comme essentiellement exogènes (Halmiton, 2003). Ces fluctuations étaient grandement associées aux évolutions des politiques entreprises par les grands pays producteurs de pétrole. Dans ce sens,

les fluctuations des prix pétroliers s’imposaient aux agents économiques. Elles ne résultent pas de leur comportement. Les fluctuations des prix pétroliers étaient surtout induites par des facteurs liés à l’offre de production. Toutefois, depuis les années 70, il devient de plus en plus clair que ces fluctuations sont également déterminées par des facteurs liés à la demande. Ainsi, l’exogénéité de ces fluctuations est de plus en plus remise en cause et les facteurs liés à l’offre montraient leur limite à expliquer les fluctuations connues après les années 70.

En utilisant un modèle SVAR, Kilian (2009) montre que les facteurs liés à l’offre n’expliquent qu’une petite partie de l’évolution des prix pétroliers. La grande partie des fluctuations que connaissent les prix des produits pétroliers est due à des facteurs liés à la demande. Les travaux de Kilian et Murphy (2012) aboutissent aux mêmes conclusions montrant que les facteurs liés à l’offre n’expliquent qu’une petite fraction des fluctuations des prix des produits pétroliers. Plus encore, Aastveit (2014) contribue à cette littérature en usant d’un modèle FAVAR. Ces résultats confirment et vont dans le sens des travaux précédents en montrant que les composantes liées à la demande sont de loin celles qui expliquent les fluctuations des prix des produits pétroliers.

Néanmoins, les recherches récentes de Baumeister et Hamilton (2018) contrastent de nouveau avec les travaux de Kilian (2009) et de Kilian et Murphy (2012) entre autres. En effet, leurs résultats indiquent que la dynamique des prix pétroliers est largement déterminée par des facteurs liés à l’offre. Les travaux de Herrera et Rangaraju (2018) rappellent alors l’importance de la nature des hypothèses des modèles utilisés. En effet, ils indiquent qu’à court terme, une élasticité faible de l’offre accroît l’importance des facteurs liés à la demande dans la fluctuation des prix pétroliers mais en revanche, à plus long terme, une élasticité plus forte de l’offre la réduit. Dans ce sens, et notamment avec la crise du Covid-19, la littérature est amenée à se questionner sur la façon dont un niveau élevé d’incertitude financière peut altérer l’élasticité des prix des produits pétroliers (Albulescu, 2020 ; Bakas et Triantafyllou, 2020). En effet, lorsque la demande ou l’offre est supposée constante, une élasticité plus faible de la demande est due à un niveau de volatilité élevé des prix pétroliers (Van Robays, 2016). Ainsi, les fluctuations des prix des produits pétroliers sont mieux expliquées par les facteurs liés à la production car l’élasticité des prix de la demande est plus faible (Baumeister et Peersman, 2013). Les résultats de Alana et Monge (2020) sur le rôle de l’incertitude en considérant le cas du Covid-19, montrent alors que les effets sur la dynamique des prix pétroliers peuvent perdurer dans le temps même si l’incertitude est transitoire.

Concernant les conséquences des fluctuations des prix pétroliers sur l’activité économique, plusieurs travaux s’y sont attelés notamment Mork (1989) et Hooker (1996). Mork (1989) montre que les fluctuations à la hausse des prix pétrolier dépriment l’activité économique tandis-que celles à la baisse n’ont pas d’impact significatif sur l’activité économique. Les travaux plus récents depuis la décennie 2000 vont dans le même sens (Herrera et al, 2019) même si Hooker (1996) et Hamilton (1996) montrent que cette relation décrite par Mork (1989) n’est pas stable dans le temps. En utilisant un modèle non linéaire, Kilian et Vigfusson (2011) montrent que l’activité économique est impactée autant par les fluctuations à la hausse que des fluctuations à la baisse des prix pétroliers.

Plus encore, la littérature relève les conséquences que peuvent avoir les fluctuations des prix pétroliers sur le niveau de consommation des ménages. En étudiant l’effet d’une hausse des prix pétroliers sur la demande agrégée, Edelstein et Kilian (2009) aboutissent à un effet dépressif. Ainsi, les fluctuations à la hausse ont tendance à contracter le niveau de la demande agrégée. Néanmoins, Alsalman et Karaki (2018) montrent la nécessité d’étudier différentes composantes de la demande agrégée. Ainsi, la composante de la demande des biens durables est celle qui est la plus impactée négativement par les fluctuations à la hausse des prix des produits pétroliers. En revanche d’autres composantes de la demande comme celle de biens non-durables sont stimulées par les fluctuations à la hausse des prix pétroliers. Lee et al (2011) quant à eux étudient les conséquences des fluctuations des prix pétroliers sur les niveaux d’investissement. Leurs travaux concluent à un effet négatif de la hausse des prix pétroliers sur les investissements. Mais leurs résultats montrent que ces effets ne sont pas immédiats. Edelstein et Kinian (2007) quant à eux relèvent la nécessité de distinguer les secteurs d’activité. Ainsi, les fluctuations à la hausse des prix des produits pétroliers n’ont pas le même impact selon le secteur d’activité considéré. Ceci montre l’effet asymétrique de ces fluctuations sur le niveau d’investissement. Ainsi, les secteurs intensifs en produits pétroliers voient les investissements dans leurs secteurs diminués tandis que les secteurs moins intensifs en ces produits peuvent connaître des niveaux d’investissement plus élevés. Ces résultats sont renforcés par les travaux de Baumeister et al (2018) qui aboutissent aux mêmes conclusions.

La littérature économique nous permet ainsi d’entrevoir aisément les enjeux liés aux fluctuations des prix énergétiques et plus particulièrement ceux des produits pétroliers. Les conséquences liées aux fluctuations de ces prix sont de plusieurs ordres et peuvent grandement contracter l’activité économique au sein des nations. Une hausse des prix pétroliers peut avoir un effet dépressif sur la consommation et le niveau d’investissement. Nonobstant les tendances

inflationnistes qu’elle peut générer, elle peut changer les structures des économies en déviant la consommation et les investissements de certains secteurs au profit d’autres secteurs. Cette nécessité d’appréhender au mieux la dynamique des prix des produits pétroliers et de prévoir ses valeurs futures s’est encore renforcée avec la récente crise liée à la pandémie du Covid-19. Ce dossier s’inscrit donc dans cette démarche en utilisant la base « oil.price » fournie par le

« Package TSA » du logiciel R studio. Cette base décrit les données mensuelles des prix du pétrole aux Etats-Unis de 1986 à 2006. À travers ce dossier, nous déterminons en premier la nature de la dynamique des prix pétroliers. Pour ce faire, la méthode à mémoire longue avec des techniques classiques basées sur l’estimation des processus AR, MA, ou ARMA est mobilisée. Nous étudions ensuite la qualité de notre modèle à décrire correctement la série empirique des prix pétroliers.

2.      Fondements économétriques

Cette partie vise à présenter l’approche économétrique adoptée. Elle s’étale sur le processus stationnaire d’une série chronologique en statuant sur un modèle AR (p) et un modèle ARIMA(p,d,q). Ensuite, nous nous s’attarderons sur la factorisation du polynôme caractéristique d’un modèle ARIMA. Enfin, de présenter le modèle ARIMA et les séries temporelles à longue mémoire.

Une série chronologique est une série de séquences de données observées à des intervalles de temps réguliers. Elle est dite stationnaire si les propriétés statistiques de la série ne changent pas au fil du temps, c’est-à-dire si la moyenne, la variance et la covariance entre les observations ne dépendent pas du temps. Les modèles de la forme Yt=Ut + Xt ou Ut est une fonction de moyenne non-constante et Xt une série stationnaire de moyenne zéro.

2.1.   Présentation du modèle AR (1)

Le modèle AR (1) est un modèle autorégressif d’ordre 1. Dans ce modèle, la valeur actuelle d’une série chronologique dépend linéairement de sa valeur précédente, pondérée par un coefficient appelé le paramètre autorégressif (AR) notée ∅. Ce dernier est généralement compris entre -1 et 1 pour assurer que le processus est stationnaire. Si |∅| est strictement inférieur à 1, la série est dite stationnaire et les prévisions peuvent être réalisées sans aucun doute en tenant compte de la moyenne et de la variance de la série. Si |∅| est supérieur ou égale à 1, le processus est explosif et la série chronologique n’est pas stationnaire.

Cependant, le modèle AR (1) ne peut pas être utilisé pour prendre en compte une autocorrélation à plus long terme, mais peut être utilisé pour modéliser des séries présentant une certaine autocorrélation à court terme. Dans le cas de la non stationnarité, la différenciation permet de stationnariser la série.

Considérons le modèle AR (1) suivant :

𝑌_𝑡 = ∅𝑌_𝑡−1 + 𝜀_𝑡 avec 𝑌_𝑡 = 𝑃𝑟𝑖𝑥 𝑑𝑢 𝑝é𝑡𝑟𝑜𝑙𝑒

On suppose que 𝜀_𝑡 est une vraie innovation c’est-à-dire qu’il n’existe pas une corrélation entre

𝜀_𝑡 et 𝑌_𝑡−1, 𝑌_𝑡−2. Afin de rendre stationnaire notre série chronologique, nous avons utilisé la méthode de la stationnarité par différenciation. L’idée est de prendre la différence entre les observations successives de notre série afin d’éliminer une tendance ou une saisonnalité.

Plus formellement, notre différence première est définie comme suit :

∇𝑌_𝑡 = 𝑒_𝑡

Cette méthode est couramment utilisée pour éliminer une tendance linéaire. Il est important de noter que celle-ci peut affecter la structure de la dépendance temporelle de la série et peut également augmenter la variabilité de la série chronologique différenciée, ce qui peut nécessiter une transformation supplémentaire, telle que la transformation de Box-Cox pour rendre la série stationnaire.

2.2.   Présentation du modèle ARIMA

Le modèle ARIMA (Autorégressif Integrated Moving Average) est un modèle de série temporelle très utilisé pour modéliser des données temporelles qui présentent une saisonnalité et/ou une tendance et prend aussi en compte les différences temporelles. Il est représenté par trois paramètres, ARIMA (p,d,q) :

• P représente l’ordre de l’autorégression (AR) permettant de mesurer la dépendance de la variable à prédire et ses propres valeurs retardées.
• D : l’ordre de différenciation qui nous indique le nombre de fois que la série doit être différenciée pour être stationnaire. Ce dernier est une propriété importante des séries temporelles et nécessite une moyenne constante et une variance finie. Si la série semble avoir une tendance à long terme, tel est notre cas, il est important de prendre une différence première pour éliminer la tendance. De même, si elle présente une tendance saisonnière, il peut être favorable de tenir compte d’une différence saisonnière.

• Q : l’ordre de la moyenne mobile (MA) qui mesure la dépendance de la variable à prédire avec l’erreur de prédiction passée.

L’écriture d’un modèle ARIMA (p,1,q)

𝑌𝑡 − 𝑌𝑡−1 = ∅1(𝑌𝑡−1 − 𝑌𝑡−2) + ∅2(𝑌𝑡−2 − 𝑌𝑡−3) + ⋯ + ∅𝑃(𝑌𝑡−𝑃 − 𝑌𝑡−𝑃−1) + 𝑒𝑡 − 𝜃1𝑒𝑡−1

− 𝜃2𝑒𝑡−2 − ⋯ − 𝜃𝑝𝑒𝑡−𝑞

𝑌_𝑡 = (1 + ∅₁)𝑌_𝑡−1 + (∅₂ − ∅₁)𝑌_𝑡−2 + (∅₃ − ∅₂)𝑌_𝑡−3 + ⋯ + (∅_𝑃 − ∅_𝑃−1)𝑌_𝑡−𝑃 − ∅_𝑃𝑌_{𝑡−𝑃−1}

+ 𝑒𝑡 − 𝜃1𝑒𝑡−1 − 𝜃2𝑒𝑡−2 − ⋯ − 𝜃𝑝𝑒𝑡−𝑞

Avec 𝒀_𝒕= prix du pétrole

En économétrie, le modèle ARIMA (p,1, q) permet de modéliser certaines séries temporelles comme les prix, le PIB, le taux d’intérêt afin d’étudier leur comportement dans le temps et de faire des prévisions. La différence première nous permet de rendre notre série chronologique stationnaire tandis que le modèle ARMA(p.q.) nous permet de décrire la structure de la stationnarité.

Ce modèle nous permet de capturer les effets à court terme et les effets à long terme c’est-à- dire les coefficients de moyennes mobiles et les coefficients d’autorégression respectivement. Elle permet également de corriger la non-stationnarité par la différence première. Le terme d’erreur blanc 𝜀_𝑡 capture tout effet imprévu ou résiduel qui n’est pas expliqué par les termes d’autorégression ou de moyenne mobile.

Le terme ∅_𝑖 mesure l’impact à long terme des valeurs passées de ∇𝑌_𝑡 sur la présence première de la série chronologique à l’instant t, tandis que le terme 𝜃_𝑝 mesure l’impact à court terme des erreurs passées et actuelles sur la différence première de la chronologique à l’instant t.

2.3.   Factorisation de polynômes caractéristiques pour un processus ARIMA(p,1,q)

La factorisation de polynômes caractéristique est importante, car il permet de savoir si le processus est stationnaire ou non-stationnaire. En effet, si toutes les racines sont en dehors du cercle unitaire, alors le processus est stationnaire. Par ailleurs, si au moins une racine se trouve à l’intérieur du cercle unitaire, donc le processus est non-stationnaire. Ce dernier n’est pas en équilibre statistique, et donc il n’est pas possible de confirmer qu’il se prolonge indéfiniment dans le passé.

𝑡

𝑌_𝑡 = ∑ 𝑊𝑗

𝑗=−𝑚

Les expressions suivantes représentent la série temporelle en termes de la somme cumulée des différences Wt à chaque période de temps. Spécialement, la somme est prise sur toutes les périodes de temps passées et présentes jusqu’à t, et pour chaque période la somme cumulée des différences West calculée.

𝑌𝑡 = ∑

𝑡

𝑗=−𝑚

𝑗

∑

𝑖=−𝑚

𝑊𝑖

𝑗=0

= 𝑌_𝑡 = ∑^𝑡+𝑚(𝑗 + 1)𝑊_𝑡−𝑗

La première équation indique la somme cumulée à partir du temps t=-m, qui est considéré comme un point arbitraire avant le début de la série temporelle. La deuxième réécrit simplement la première équation en remplaçant l’indice j par j+1, de sorte que la somme commence en j=0

En général, cette expression n’a pas de forme explicite simple en termes des paramètres ARMA de la série temporelle. Cependant, elle peut être utile pour certaines analyses et pour l’expression de Yt en termes de la série sous-jacente (Wt).

2.4.   Modèle ARIMA et série temporelle à mémoire longue

Enfin, les modèles ARIMA sont utilisés pour modéliser des séries temporelles à mémoire longue. Ces dernières sont celles où les évènements passés ont une influence sur des évènements actuels, mais ces effets diminuent lentement au fil du temps. En effet, la propriété de stationnarité pour pouvoir appliquer des modèles statistiques et identifier les tendances et les motifs dans les données. Par ailleurs, la différenciation est utilisée pour éliminer les tendances qui ne sont pas stationnaires.

Pour les séries temporelles à mémoire longue, les modèles ARIMA sont privilégiés aux modèles ARMA car ils peuvent capturer la dynamique de longue durée de la série. Cela est possible grâce à l’utilisation du processus intégré permettant de prendre en compte les effets à long terme des événements passés.

3.      Résultats et interprétations

Cette section décrit les résultats des estimations. La première partie est consacrée à l’étude de la stationnarité et à la détermination de l’ordre d’intégration de notre série. Ensuite, la deuxième

partie étudie les fonctions d’autocorrélation et d’autocorrélation partielles. Enfin, la troisième partie présente les estimations des différents modèles considérés.

3.1.   Stationnarité et ordre d’intégration

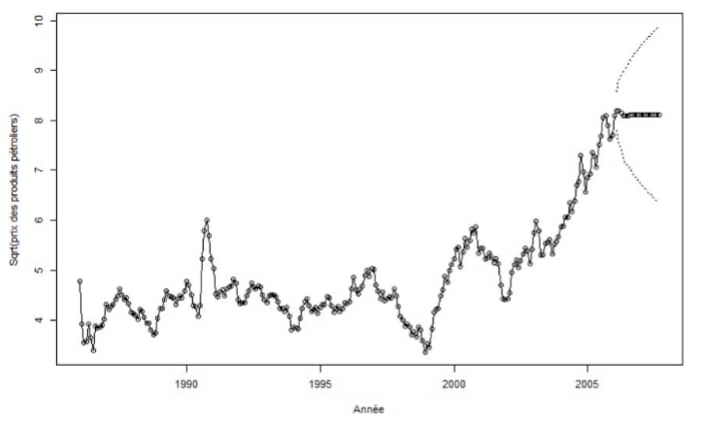
La figure 1 présente l’évolution du prix du pétrole sans différence (Fig 1a) et en différence première (Fig 1b). L’analyse de la Fig 1a montre un premier pic du prix du pétrole juste après les années 1990 puis une tendance soutenue à la hausse depuis les années 2002. Globalement, cette série varie grandement entre 1986 et 2006. Elle n’est donc pas stationnaire. Dans ce sens, une première transformation de cette série est faite à partir de la fonction logarithmique qui permet de stationnariser en variance. Ensuite la Fig 1b présente l’évolution de la différence première du logarithme du prix du pétrole. On voit que sur la Fig 1b, la série présente une structure plus homogène. Cette tendance retranscrit une série stationnaire dont l’ordre d’intégration est égal à 1.

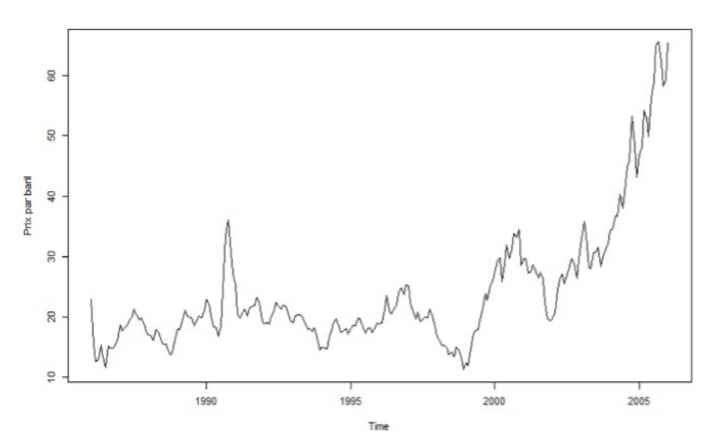
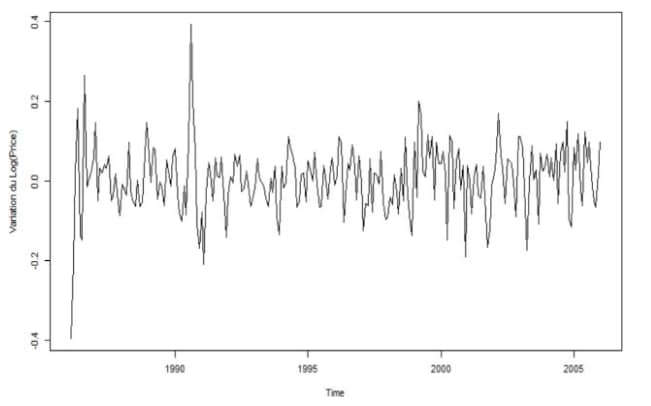
Source. Auteurs à partir des données de la base « oil.price » du package « TSA » de Rstudio

3.2.   Détermination du nombre de retards

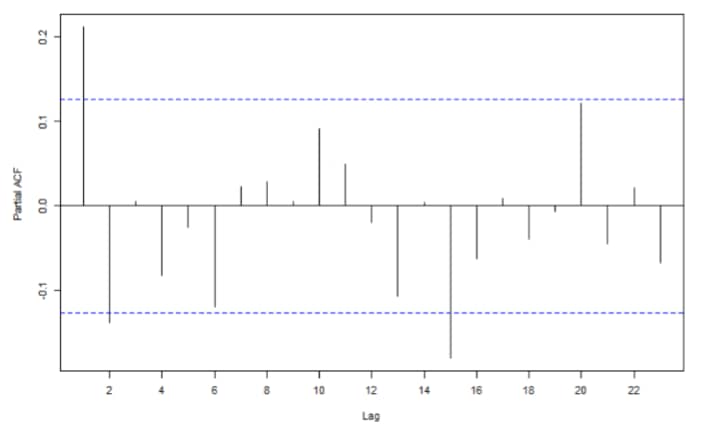
La Figure 2 retrace les fonctions d’autocorrélation (Fig 2a et 2c) et d’autocorrélation partielles (Fig 2b et 2d). La fonction d’autocorrélation pour les prix pétroliers décroît assez lentement (Fig 2a) tandis que la Fig 2c indique et suggère un processus MA (1) pour la différence du logarithme des prix du pétrole. En effet, la fonction d’autocorrélation détermine la mémoire d’un processus MA. La fonction d’autocorrélation quant à lui (Fig 2d) suggère plusieurs ordres de retard possibles pour un AR. En considérant les pics au retard 15 et 20, on opte pour un AR (4).

Dans la mesure où le logarithme des prix pétroliers a été différencié une fois pour rendre la série stationnaire, les résultats de la Figure 2 nous amènent à opter pour des processus IMA(1,1) et ARI(4,1) afin de modéliser la dynamique des prix pétroliers. Néanmoins, afin de prendre en compte toute l’information fournie par les fonctions d’autocorrélation et d’autocorrélation partielles, une combinaison des deux processus peut sembler plus judicieuse. Dans ce sens, en plus de l’estimation d’un IMA (1,1) et d’un AR (4,1), nous procédons à l’estimation d’un ARIMA (4,1,1).

Figure 2. Fonctions d’autocorrélation et d’autocorrélation partielles

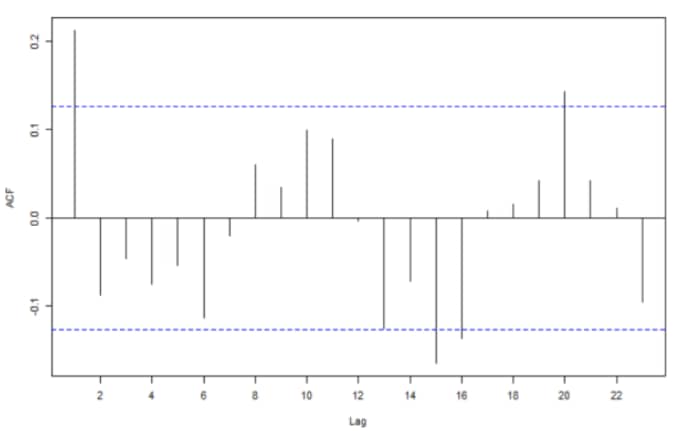
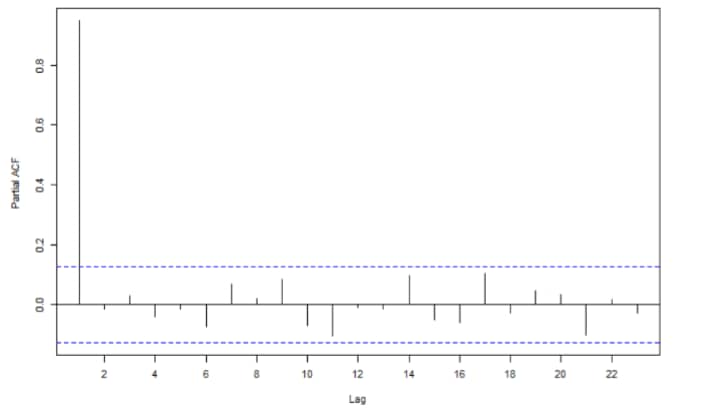
Source. Auteurs à partir des données de la base « oil.price » du package « TSA » de Rstudio

3.3.   Estimation des paramètres

La Table 1 présente les estimations des trois modèles. En guise de robustest, les coefficients sont estimés à travers la méthode des moindres carrés conditionnels et par la méthode de maximum de vraisemblance. Les coefficients estimés au niveau des trois modèles sont tous en dessous de 1. Comparativement au modèle ARIMA, le modèle IMA sous-estime l’effet des valeurs retardées sur la fluctuation des prix du pétrole. Les résultats s’inversent lorsqu’on

compare le modèle ARIMA au modèle ARI. De plus, le sens de l’effet des valeurs retardées n’est pas le même. Les résultats indiquent que le ARIMA est le modèle qui minimise le plus le critère AIC. Le principe de parcimonie nous amène donc à choisir le modèle ARIMA (4,1,1) comme celui qui modélise le mieux la dynamique des prix du pétrole.

Table 1. Estimation des paramètres

IMA (0,1,1)			ARI (4,1,0)		ARIMA (4,1,1)
	Méthodes des moindres carrés conditionnels	Maximum de maximum vraisemblance	Méthodes des moindres carrés conditionnels	Maximum de maximum vraisemblance	Méthodes des moindres carrés conditionnels	Maximum de maximum vraisemblance
MA (1)	0,2731	0,2956			0,3176	0,5112
	(0,0681)	(0,0693)			(0,1811)	(0,3382)
AR (1)			0,2169	0,2673	-0,0907	-0,2383
			(0,0639)	(0,0669)	(0,1859)	(0,3438)
AR (2)			-0,127	-0,155	-0,0578	-0,0209
			(0,0653)	(0,0691)	(0,0737)	(0,1143)
AR (3)			0,0616	0,0238	0,0283	-0,0503
			(0,065)	(0,0691)	(0,0681)	(0,088)
AR (4)			-0,0871	-0,097	-0,0843	-0,0903
			(0,0607)	(0,0681)	(0,0602)	(0,0719)
Variance du terme d’erreur	0,0067	0,0067	0,0059	0,0066	0,0059	0,0065
Log-likelihood	259,58	260,29	274,7	261,82	275,75	262,02
Critère AIC		-518,58		-515,64		-514,04

Note. Erreurs standards entre parenthèses

La Figure 3 retrace l’évolution des prix du pétrole à travers le modèle empirique ARIMA(4,1,1). La dynamique décrite est assez similaire à celle des données empiriques de la Figure 1a. Ceci atteste de la qualité de notre modèle pour prédire les valeurs des prix pétroliers. De plus le test de bruit blanc (Fig 3b) assure la normalité des résidus.

Figure 3. Qualité du modèle

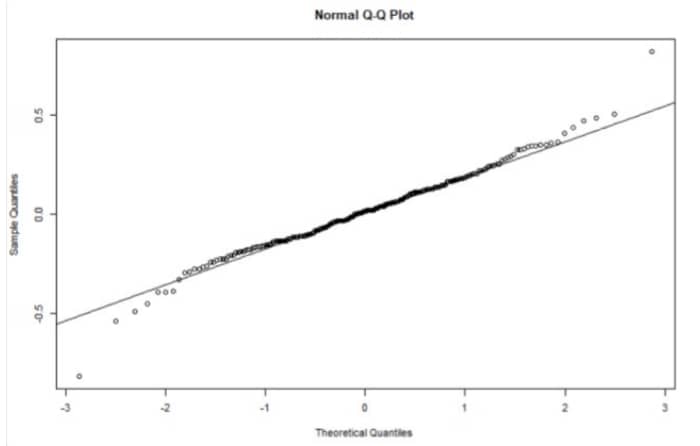
Source. Auteurs à partir des données de la base « oil.price » du package « TSA » de Rstudio

CONCLUSION

Notre objectif à travers ce dossier était d’appréhender la nature de la dynamique des prix pétroliers. Pour ce faire, nous avons adopté la méthode à mémoire longue avec des techniques classiques basées sur l’estimation des processus AR, MA, ou ARMA. Nos résultats montrent que la série des prix du pétrole est stationnaire en première différence. L’analyse des fonctions d’autocorrélation et d’autocorrélation partielles nous a amené à estimer trois modèles à savoir un ARI (4,1,0), un IMA (0,1,1) et un ARIMA (4,1,1). Sur la base du principe de parcimonie, le modèle ARIMA (4,1,1) s’impose comme celui qui décrit le mieux la dynamique des prix pétroliers. Eu égard des enjeux liés à la dynamique économique, ce modèle permet alors d’appréhender la nature des fluctuations que connaissent les prix du pétrole et de prévoir du mieux possible son évolution.

RÉFERENCES

Aastveit, K. (2014). Oil Price Shocks in a Data-rich Environnement. Energy Economics, 45, 268-279.

Alana, L., & Monge, M. (2020). Crude Oil Prices and Covid-19 : Persistence of the Shock.

Albulescu, C. (2020). Coronavirus and Oil Price Crash. Electronic Journal.

Alsalman, Z., & Karaki, M. (2018). Oil Prices and Personal Consumption Expenditures : Does the Source of the Shock Matter ? Oxford Bulletin of Economics and Statistics.

Bakas, D., & Triantafyllou, A. (2020). Commodity Price Volatility and the Economic Uncertainty of Pandemics. Electronic Journal.

Baumeister, C., & Hamilton, J. (2018). Structural Interpretation of Vector Autoregressions with Incomplete Identification : Revisiting the Role of Oil Supply and Demand Shocks. American Economic Review.

Baumeister, C., & Peersman, G. (2013). The Role of Time-Varying Price Elasticities in Accounting for Volatility Changes in the Crude Oil Market. Journal of Applied Econometrics, 28(7), 1087-1109.

Baumeister, C., Kilian, L., & Zhou, X. (2018). Is the Discretionary Income Effect of Oil Price Shocks a Hoax ? The Energy Journal .

Edelstein, P., & Kilian, L. (2007). The Response of Business Fixed Investment to Changes in Energy Prices : A Test of Some Hypotheses About the Transmission of Energy Price Shocks. Journal of Macroeconomics, 7(1).

Edelstein, P., & Kilian, L. (2009). How Sensitive are Consumer Expenditures to Retail Energy Prices ? Journal of Monetary Economics, 56(6), 766-779.

Hamilton, J. (1996). This is What Happened to the Oil Price-Macroeconomy Relationship.

Journal of Monetary Economics, 38(2), 215-220.

Hamilton, J. (2003). What Is an Oil Shock. Journal of Econometrics, 2(113), 363-398. Herrera, A. M., Karaki, M., & Rangaraju, S. (2019). Oil Price Shocks and US. Economic

Activity. Energy Policy(129), 89-99.

Herrera, A., & Rangaraju, S. (2018). The Effect of Oil Supply Shocks on US Economic Activity

: What Have We Learned ? University of Kentucky.

Hooker, M. (1986). What Happened to the Oil Price-Macroeconomy Relationship ? Journal of Monetary Economics, 38(2), 195-213.

Kilian, L. (2009). Not All Oil Price Shocks Are Alike: Disentangling Demand and Supply Shocks in the Crude Oil Market. American Economic Review, 99(3), 1053-1069.

Kilian, L., & Murphy, D. (2012). Why Agnostic Sign Restrictions Are Not Enough : Understanding the Dynamics of Oil Market VAR Moders. Journal of the European Economic Association, 10(5), 1166-1188.

Kilian, L., & Vigfusson, R. (2011). Non linearities in the Oil Price-Output Relationship.

Macroeconomics Dynamics, 15(3), 337-363.

Lee, K., Kang, W., & Ratti, R. (2011). Oil Price Shocks, Firm Uncertainty, and Investment.

Macroeconomic Dynamics, 15(3), 416-436.

Mork, K. (1989). Oil and the Macroeconomy When Prices Go Up and Down : An Extension of Hamilton’s Results. Journal of Political Economy, 97(3), 740-744.

Van Robays, I. (2016). Macroeconomic Uncertainty and Oil Price Volatility. Oxford Bulletin of Economics and Statistics, 78(5), 671-693.

Par Anderson DENART, étudiant masterant en analyse et politique économique: statistique et économétrie, à l’Université de Strasbourg.